Printable version

Lesson 9-4 - Geometry's Most Elegant Theorem

Today, we covered the most famous of geometric theorems:

With the Altitude-on-Hypotenuse Theorem, the proof is pretty straight forward:

The converse is also true, and is useful in terms of classifying triangles:

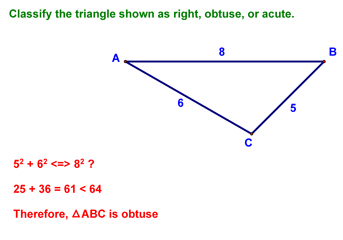
Here's an example of how we might use this theorem:

Another example follows: